Geometría - Ángulos
Ángulos
1 – La suma de las medidas de dos ángulos es 140° y el duplo del complemento del primero es igual al triple del complemento del complemento del suplemento del doble del segundo ángulo. Determinar el mayor ángulo.
Ejercicio 1:
La suma de las medidas de dos ángulos es 140° y el duplo del complemento del primero es igual al triple del complemento del complemento del suplemento del doble del segundo ángulo. Determinar el mayor ángulo.
Ejercicio 4:
La suma de las medidas de dos ángulos es 140° y el duplo del complemento del primero es igual al triple del complemento del complemento del suplemento del doble del segundo ángulo. Determinar el mayor ángulo.
Solución:
i) x+y=140\newline ii)2\left ( 90-x \right )=3\left ( 90-\left ( 90-\left ( 180-2y \right ) \right ) \right )Resolvemos:
2\left ( 90-x \right )=3\left ( 90-\left ( 90-180+2y \right ) \right )\newline 2\left ( 90-x \right )=3\left ( 90-\left ( -90+2y \right ) \right )\newline2\left ( 90-x \right )=3\left ( 90+90-2y \right )\newline2\left ( 90-x \right )=3\left ( 180-2y \right ) …\left (iii\right )De la ecuación i) despejamos ‘y’:
y = 140-xReemplazamos en ecuación iii):
2\left ( 90-x \right )=3\left ( 180-2\left ( 140-x \right ) \right )\newline2\left ( 90-x \right )=3\left ( 180-280+2x\right )\newline2\left ( 90-x \right )=3\left ( -100+2x\right )\newline180-2x = -300+6x\newline180+300=6x+2x\newline480 = 8x\newline x=60^{\circ}Sustituimos para encontrar el valor de ‘y’:
y = 140-x \newline y = 140-60\newline y=80^{\circ}El mayor ángulo es y=80^{\circ}
2 – Un tercio de la diferencia entre el suplemento y el complemento de un ángulo es igual al doble de su complemento. Calcular el complemento del complemento del ángulo.
Ejercicio 2:
Un tercio de la diferencia entre el suplemento y el complemento de un ángulo es igual al doble de su complemento. Calcular el complemento del complemento del ángulo.
Ejercicio 2:
Un tercio de la diferencia entre el suplemento y el complemento de un ángulo es igual al doble de su complemento. Calcular el complemento del complemento del ángulo.
Solución:
\frac{1}{3}\left [ \left ( 180-x \right )-\left ( 90-x \right ) \right ]=2\left ( 90-x \right )\newline \frac{1}{3}\left [ 180-x-90+x \right ]=2\left ( 90-x \right )\newline\frac{1}{3}\left [ 90-\cancel{x}+\cancel{x} \right ]=2\left ( 90-x \right )\newline \newline\newline 30=180-2x\newline 2x= 180-30 \newline 2x=150 \newline x=75^{\circ}Calculamos el complemento del complemento del ángulo.
= 90 -\left ( 90-x \right )\newline =90 -\left (90-75 \right )\newline= 90-15 \newline = 75^{\circ}Otra forma:
El complemento del complemento de un número es el mismo número.
CC_{75^{\circ}} = 75^{\circ}3 – Calcule el complemento de la medida de un ángulo; sabiendo que el suplemento del complemento de la medida de dicho ángulo es igual a la semisuma de su complemento con su suplemento.
Ejercicio 3:
Calcule el complemento de la medida de un ángulo; sabiendo que el suplemento del complemento de la medida de dicho ángulo es igual a la semisuma de su complemento con su suplemento.
Ejercicio 3:
Calcule el complemento de la medida de un ángulo; sabiendo que el suplemento del complemento de la medida de dicho ángulo es igual a la semisuma de su complemento con su suplemento.
Solución:
Calcular el C_{x}:, sabiendo que: SC_{x} =\frac{C_{x}+S_{x}}{2}
Reemplazando:
180-\left ( 90-x \right ) =\frac{\left ( 90-x \right )+\left ( 180-x \right )}{2}\newline 180-90+x=\frac{90-x+180-x}{2}\newline 90+x=\frac{\cancel{270}-\cancel{2}x}{\cancel{2}}\newline 90+x=135-x \newline 2x= 135-90 \newline 2x=45 \newline x=22.5^{\circ}Calculamos el C_{x}:
C_{x}= 90-22.5 \newline C_{x}=67.5^{\circ}Convertimos a grados y minutos:
Paso1 : Nos quedamos con la parte enteraque es 67°
Paso2: Transformamos la parte decimal minutos:
=0.5^{\circ}\cdot \frac{{60}'}{1^{\circ}} \newline ={30}'La respuesta sería: 67^{\circ}{30}'
4 – En una recta se ubican los puntos A,B,C y D, tal que BC = CD. Si \left ( AB \right )\left ( AD \right ) = 7-\frac{\left ( BD \right )^{2}}{4}, calcule AC.
Ejercicio 4:
En una recta se ubican los puntos A,B,C y D, tal que BC = CD. Si \left ( AB \right )\left ( AD \right ) = 7-\frac{\left ( BD \right )^{2}}{4}, calcule AC.
Ejercicio 4:
4 – En una recta se ubican los puntos A,B,C y D, tal que BC = CD. Si \left ( AB \right )\left ( AD \right ) = 7-\frac{\left ( BD \right )^{2}}{4}, calcule AC.
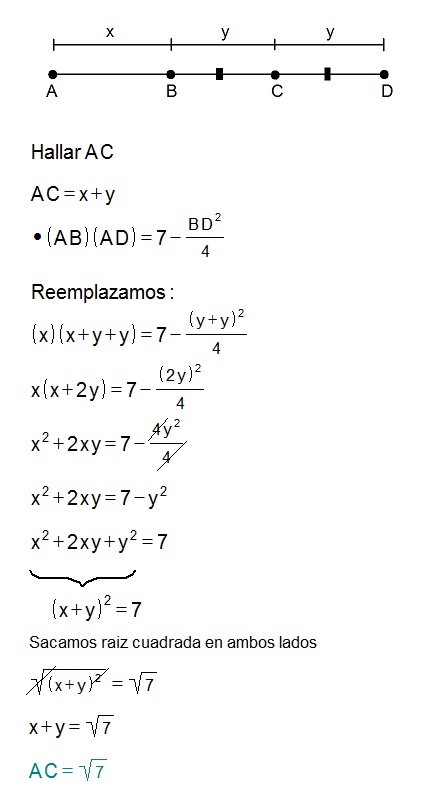
5 – En una recta se ubican los puntos consecutivos U,N,P de
manera que UN-NP=28, luego se ubican los puntos medios A de UN, C de NP y B de AC. Calcule 7BN.
Ejercicio 5:
En una recta se ubican los puntos consecutivos U,N,P de
manera que UN-NP=28, luego se ubican los puntos medios A de UN, C de NP y B de AC. Calcule 7BN.
Ejercicio 5:
En una recta se ubican los puntos consecutivos U,N,P de
manera que UN-NP=28, luego se ubican los puntos medios A de UN, C de NP y B de AC. Calcule 7BN.

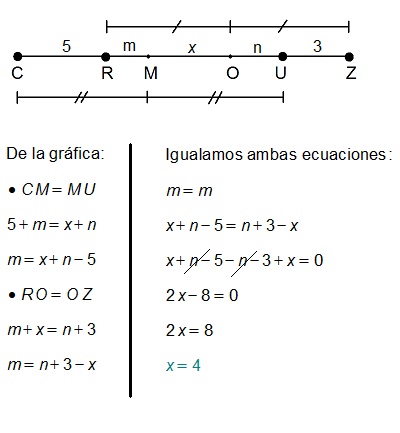
6 – Sobre una recta se ubican los puntos consecutivos C, R, U y Z, si CR = 5 y UZ = 3; hallar la distancia entre los puntos medios de RZ y CU; si ambos están entre R y U.
Ejercicio 6:
Sobre una recta se ubican los puntos consecutivos C, R, U y Z, si CR = 5 y UZ = 3; hallar la distancia entre los puntos medios de RZ y CU; si ambos están entre R y U.
Ejercicio 6:
Sobre una recta se ubican los puntos consecutivos C, R, U y Z, si CR = 5 y UZ = 3; hallar la distancia entre los puntos medios de RZ y CU; si ambos están entre R y U.
7 – Sobre una línea recta se toman los puntos consecutivos L, U, I y S tal que: LU = 8u, IS = 9u y \left ( LI \right )\left ( IS \right )+ \left ( LU \right )\left ( US \right ) = \left ( UI \right )\left ( LS \right ) . Hallar UI.
Ejercicio 7:
Sobre una línea recta se toman los puntos consecutivos L, U, I y S tal que: LU = 8u, IS = 9u y \left ( LI \right )\left ( IS \right )+ \left ( LU \right )\left ( US \right ) = \left ( UI \right )\left ( LS \right ) . Hallar UI.
Ejercicio 7:
7 – Sobre una línea recta se toman los puntos consecutivos L, U, I y S tal que: LU = 8u, IS = 9u y \left ( LI \right )\left ( IS \right )+ \left ( LU \right )\left ( US \right ) = \left ( UI \right )\left ( LS \right ) . Hallar UI.

8 – En una línea recta se consideran los puntos consecutivos L, U, I yS, los cuales forman una división armónica. Además: UI = \frac{47}{IS}, LS = \frac{96}{LU}, calcular LI.
Ejercicio 8:
En una línea recta se consideran los puntos consecutivos L, U, I yS, los cuales forman una división armónica. Además: UI = \frac{47}{IS}, LS = \frac{96}{LU}, calcular LI.
Ejercicio 8:
En una línea recta se consideran los puntos consecutivos L, U, I yS, los cuales forman una división armónica. Además: UI = \frac{47}{IS}, LS = \frac{96}{LU}, calcular LI.

9 – Sobre una recta se ubican los puntos consecutivos M, A y B siendo O el punto medio de AB. Calcule el valor de \mu ^{2} para que se cumpla la siguiente igualdad.
\frac{\left ( MA \right )^{2}+\left ( MB \right )^{2}}{\left ( MO \right )^{2}+\left ( AO \right )^{2}}=\muEjercicio 9:
Sobre una recta se ubican los puntos consecutivos M, A y B siendo O el punto medio de AB. Calcule el valor de \mu ^{2} para que se cumpla la siguiente igualdad.
\frac{\left ( MA \right )^{2}+\left ( MB \right )^{2}}{\left ( MO \right )^{2}+\left ( AO \right )^{2}}=\muEjercicio 9:
Sobre una recta se ubican los puntos consecutivos M, A y B siendo O el punto medio de AB. Calcule el valor de \mu ^{2} para que se cumpla la siguiente igualdad.
\frac{\left ( MA \right )^{2}+\left ( MB \right )^{2}}{\left ( MO \right )^{2}+\left ( AO \right )^{2}}=\mu
