Geometría - Teoría de segmentos
TEORÍA DE SEGMENTOS
I. ¿Qué es una recta?
Una recta es un conjunto de todos los puntos que siguen la misma dirección y tiene dos propiedades importantes:
- No tiene principio ni fin.
- cualquier par de puntos en la recta puede ser utilizado para definir su dirección.

II. ¿Qué es un segmento?
Un segmento es una parte de una recta comprendida entre dos puntos. Los puntos que delimitan el segmento se llaman extremos, y la longitud del segmento se puede calcular como la distancia entre estos dos puntos.

III. Teoremas
a) Punto medio
Es el punto que se encuentra exactamente a la mitad del segmento, es decir, que divide al segmento en dos partes iguales.
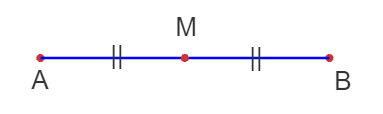
\large \overline{AM}= \overline{MB}=\frac{\overline{AB}}{2}
b) Suma o adición de segmentos
Es la unión de dos o más segmentos para formar un segmento más largo.

\large \overline{AB}+ \overline{BC}+ \overline{CD}=\overline{AD}
c) Resta o sustracción de segmentos
Es una operación que se realiza entre dos segmentos para obtener un nuevo segmento cuya longitud es la resta de las longitudes de los segmentos iniciales.

\large \overline{AD}- \overline{AC}=\overline{CD}
d) Segmento que une los puntos medios de AB y CD

\large \overline{MN} = \frac{\overline{AC}+\overline{BD}}{2}
e) División armónica de segmentos
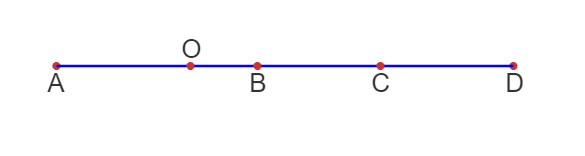
Propiedades
- Propiedad 1:
AB>BC
- Propiedad 2: Relación de Descartes
\large\frac{1}{AB}+\frac{1}{AD}=\frac{1}{AC} \large o \large \frac{1}{DC}+\frac{1}{DA}=\frac{2}{DB}
- Propiedad 3: Relación de Newton
Si O es punto medio de AC:
\large\left ( OC \right )^{2}=OB\cdot OD
- Propiedad 4:
Si se cumple que los segmentos determinados por la cuaterna armónica tienen la siguiente relación, donde n>0 :
\large \frac{AB}{BC}=n\frac{AD}{CD}
Entonces se cumple lo siguiente:
\large \frac{n+1}{AC}=\frac{n}{AB}+\frac{1}{AD}
f) Media y extrema razón de un segmento
Cuando se dice que un segmento está en media y extrema razón se refiere a un segmento que está dividido en dos partes de manera que la longitud de la parte más larga está en la misma proporción que la longitud total del segmento y la parte más corta.

Si se cumple:
\large \overline{AB}> \overline{BC}
y también:
\overline{AB}^{2} = \overline{AC}\cdot \overline{BC}
Entonces se puede decir:
- \large \overline{AB} = \left ( \frac{\sqrt{5}-1}{2} \right )\overline{AC} (AB es sección aurea de AC).
- \large \overline{AB} > \frac{\overline{AC}}{2}
- Número aúreo \large =\left ( \frac{\sqrt{5}-1}{2} \right )