Segmentos
A continuación se muestran algunos ejercicios de segmentos en diferentes niveles de dificultad. Si desea revisar la teoría de segmentos, puede hacer clic en el siguiente botón para acceder a ella.
1 – En una recta se ubican los puntos A, B, C y D, tal que
BC=CD.
Si (AB)(AD)=7-\frac{BD^{2}}{4}, calcule AC.
Ejercicio 1:
En una recta se ubican los puntos A, B, C y D, tal que BC=CD.
Si (AB)(AD)=7-\frac{BD^{2}}{4}, calcule AC.
Ejercicio 1:
En una recta se ubican los puntos A, B, C y D, tal que BC=CD.
Si (AB)(AD)=7-\frac{BD^{2}}{4}, calcule AC.
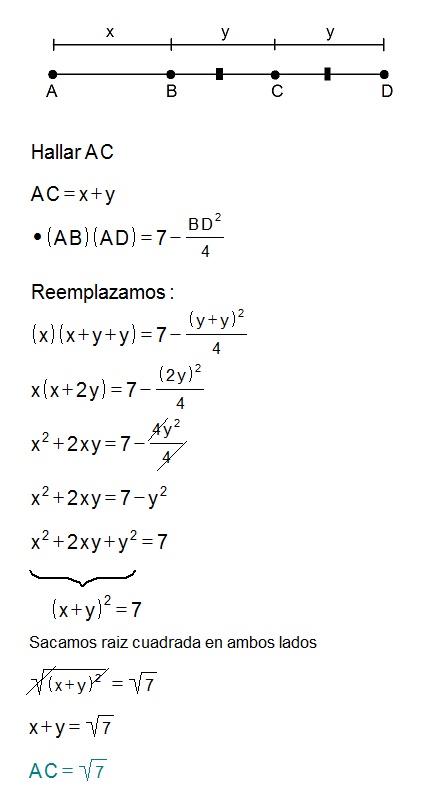
2 – En una recta se ubican los puntos consecutivos U, N, P de
manera que (\overline{UN}) – (\overline{NP}) =28, luego se ubican los puntos medios A de \overline{UN} , C de \overline{NP} y B de \overline{AC} . Calcule 7\overline{BN}.
Ejercicio 2:
En una recta se ubican los puntos consecutivos U, N, P de manera que (\overline{UN}) – (\overline{NP}) =28, luego se ubican los puntos medios A de \overline{UN} , C de \overline{NP} y B de \overline{AC} . Calcule 7\overline{BN}.
Ejercicio 2:
En una recta se ubican los puntos consecutivos U, N, P de manera que (\overline{UN}) – (\overline{NP}) =28, luego se ubican los puntos medios A de \overline{UN} , C de \overline{NP} y B de \overline{AC} . Calcule 7\overline{BN}.

3 – Sobre una recta se ubican los puntos consecutivos C,R,U,Z, Si \overline{CR}=5 y \overline{UZ}=3. Hallar la distancia entre los puntos medios de \overline{RZ} y \overline{CU} ; si ambos están entre R y U.
Ejercicio 3:
Sobre una recta se ubican los puntos consecutivos C,R,U,Z, Si \overline{CR}=5 y \overline{UZ}=3.
Hallar la distancia entre los puntos medios de \overline{RZ} y \overline{CU} ; si ambos están entre R y U.
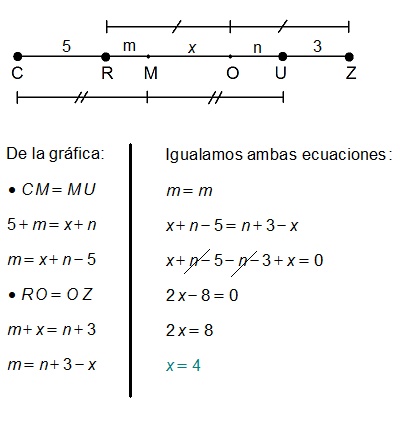
Ejercicio 3:
Sobre una recta se ubican los puntos consecutivos C,R,U,Z, Si \overline{CR}=5 y \overline{UZ}=3.
Hallar la distancia entre los puntos medios de \overline{RZ} y \overline{CU} ; si ambos están entre R y U.
4 – Sobre una línea recta se toman los puntos consecutivos L ,U , I y S tal que: \overline{LU} =8u , \overline{IS} = 9u y (\overline{LI}) (\overline{IS})+(\overline{LU})(\overline{US})=(\overline{UI})(\overline{LS}). Hallar \overline{UI}.
Ejercicio 4:
Sobre una línea recta se toman los puntos consecutivos L ,U , I y S tal que: \overline{LU} =8u ,
\overline{IS} = 9u y (\overline{LI}) (\overline{IS})+(\overline{LU})(\overline{US})=(\overline{UI})(\overline{LS}). Hallar \overline{UI}.
Ejercicio 4:
Sobre una línea recta se toman los puntos consecutivos L ,U , I y S tal que: \overline{LU} =8u ,
\overline{IS} = 9u y (\overline{LI}) (\overline{IS})+(\overline{LU})(\overline{US})=(\overline{UI})(\overline{LS}). Hallar \overline{UI}.

5 – En una línea recta se consideran los puntos consecutivos L, U, I y S los cuales forman una división armónica. Además: \overline{UI}=\frac{47}{\overline{IS}}, \overline{LS}=\frac{96}{\overline{LU}}, calcular \overline{LI}.
Ejercicio 5:
En una línea recta se consideran los puntos consecutivos L, U, I y S los cuales forman una división armónica. Además: \overline{UI}=\frac{47}{\overline{IS}}, \overline{LS}=\frac{96}{\overline{LU}}, calcular \overline{LI}.
Ejercicio 5:
En una línea recta se consideran los puntos consecutivos L, U, I y S los cuales forman una división armónica. Además: \overline{UI}=\frac{47}{\overline{IS}}, \overline{LS}=\frac{96}{\overline{LU}}, calcular \overline{LI}.

6 – Sobre una recta, se ubican los puntos consecutivos M, A y B siendo O el punto medio de \overline{AB} . Calcule el valor de \mu^{2} para que se cumpla la siguiente igualdad.
\frac{(\overline{MA})^{2}+(\overline{MB})^{2}}{(\overline{MO})^{2}+(\overline{AO})^{2}}=\muEjercicio 6:
Sobre una recta, se ubican los puntos consecutivos M, A y B siendo O el punto medio de \overline{AB} . Calcule el valor de \mu^{2} para que se cumpla la siguiente igualdad.
\Large{\frac{(\overline{MA})^{2}+(\overline{MB})^{2}}{(\overline{MO})^{2}+(\overline{AO})^{2}}=\mu}Ejercicio 6:
Sobre una recta, se ubican los puntos consecutivos M, A y B siendo O el punto medio de \overline{AB} . Calcule el valor de \mu^{2} para que se cumpla la siguiente igualdad.
\Large{\frac{(\overline{MA})^{2}+(\overline{MB})^{2}}{(\overline{MO})^{2}+(\overline{AO})^{2}}=\mu}
7 – Sobre una línea recta se toman los puntos consecutivos A ,B , C y D, tal que: (\overline{AB})(\overline{CD})=(\overline{AD})(\overline{BC}); \frac{\overline{BC}}{7}=\frac{4}{\overline{CD}} y \overline{CD}-7=\overline{BC} . Calcule \overline{AC}.
Ejercicio 7:
Sobre una línea recta se toman los puntos consecutivos A ,B , C y D, tal que:
(\overline{AB})(\overline{CD})=(\overline{AD})(\overline{BC}); \frac{\overline{BC}}{7}=\frac{4}{\overline{CD}} y \overline{CD}-7=\overline{BC}.
Calcule \overline{AC}.
Ejercicio 7:
Sobre una línea recta se toman los puntos consecutivos A ,B , C y D, tal que:
(\overline{AB})(\overline{CD})=(\overline{AD})(\overline{BC}); \frac{\overline{BC}}{7}=\frac{4}{\overline{CD}} y \overline{CD}-7=\overline{BC}.
Calcule \overline{AC}.

8 – En una línea recta se tienen los puntos consecutivos L, A, S siendo \overline{LS}=10u, luego se ubican los puntos medios I, D, E, P de \overline{LA}, \overline{AS}, \overline{LD} y \overline{IS} respectivamente . Calcular \overline{EP}.
Ejercicio 8:
En una línea recta se tienen los puntos consecutivos L, A, S siendo \overline{LS}=10u,
luego se ubican los puntos medios I, D, E, P de \overline{LA}, \overline{AS}, \overline{LD} y \overline{IS} respectivamente.
Calcular \overline{EP}.
Ejercicio 8:
En una línea recta se tienen los puntos consecutivos L, A, S siendo \overline{LS}=10u,
luego se ubican los puntos medios I, D, E, P de \overline{LA}, \overline{AS}, \overline{LD} y \overline{IS} respectivamente.
Calcular \overline{EP}.

