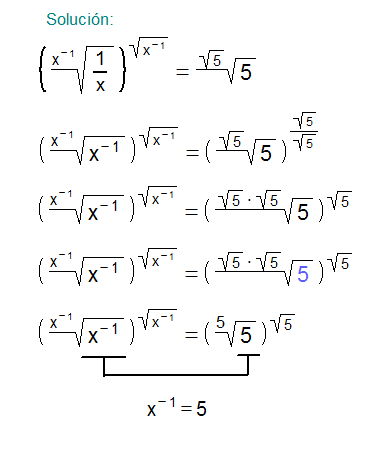Álgebra - Ecuaciones
Álgebra - Ecuaciones
1 – Efectuar
\footnotesize{E=\sqrt{27^{-3^{-1}}+36^{-2^{-1}}+\left ( \frac{4}{3}\right )^{-1}-2^{-2}}}
Ejercicio 1:
1 – Efectuar
\Large{E=\sqrt{27^{-3^{-1}}+36^{-2^{-1}}+\left ( \frac{4}{3}\right )^{-1}-2^{-2}}}
Ejercicio 1:
1 – Efectuar
\Large{E=\sqrt{27^{-3^{-1}}+36^{-2^{-1}}+\left ( \frac{4}{3}\right )^{-1}-2^{-2}}}
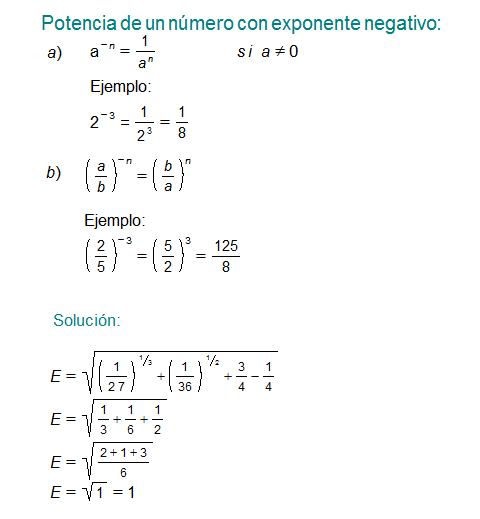
2 – Efectuar
\scriptsize {E=\sqrt{\left [ \left ( -27 \right )^{-\frac{2}{3}}+\left ( 27 \right )^{-\frac{5}{3}}+2\left ( 3 \right )^{-4} \right ]^{-0.2}}}
Ejercicio 2:
2 – Efectuar
\Large{E=\sqrt{\left [ \left ( -27 \right )^{-\frac{2}{3}}+\left ( 27 \right )^{-\frac{5}{3}}+2\left ( 3 \right )^{-4} \right ]^{-0.2}}}
Ejercicio 2:
2 – Efectuar
\Large{E=\sqrt{\left [ \left ( -27 \right )^{-\frac{2}{3}}+\left ( 27 \right )^{-\frac{5}{3}}+2\left ( 3 \right )^{-4} \right ]^{-0.2}}}
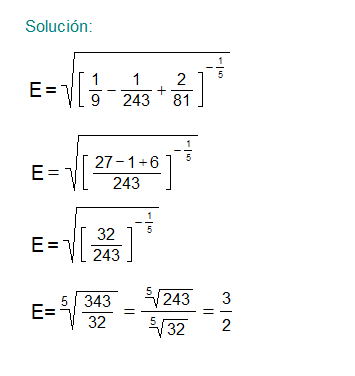
3 – Simplificar
\Large{H=\frac{2^{n-1}\cdot 4^{-2n+1}+8^{-n+2}}{16\left ( 2^{n} \right )^{-3}}}
Ejercicio 3:
Simplificar
\huge{H=\frac{2^{n-1}\cdot 4^{-2n+1}+8^{-n+2}}{16\left ( 2^{n} \right )^{-3}}}
Ejercicio 3:
Simplificar
\Large{H=\frac{2^{n-1}\cdot 4^{-2n+1}+8^{-n+2}}{16\left ( 2^{n} \right )^{-3}}}

4 – Simplificar
\Large{E=\left [ \left ( \frac{1}{64} \right )^{-2^{-1}} \right ]^{\left ( -27 \right )^{-3^{-1}}}}
Ejercicio 4:
Simplificar
\LARGE{E=\left [ \left ( \frac{1}{64} \right )^{-2^{-1}} \right ]^{\left ( -27 \right )^{-3^{-1}}}}
Ejercicio 4:
Simplificar
\LARGE{E=\left [ \left ( \frac{1}{64} \right )^{-2^{-1}} \right ]^{\left ( -27 \right )^{-3^{-1}}}}
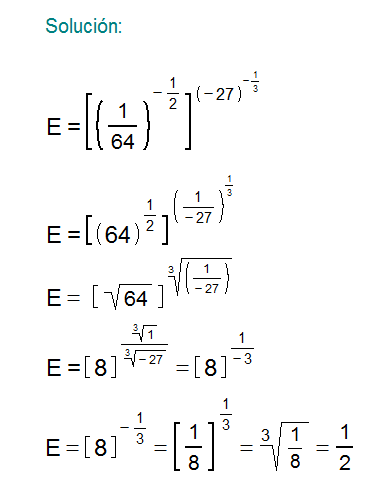
5 – Hallar 'x' si:
\Large{7^{3x-2}+7^{2}=50}
Ejercicio 5:
Hallar 'x' si:
\LARGE{7^{3x-2}+7^{2}=50}
Ejercicio 5:
Hallar 'x' si:
\Large{7^{3x-2}+7^{2}=50}

6 – Simplificar
\huge{H=\sqrt[{\sqrt[\sqrt{2}]{4}}]{2^{2^{\sqrt{2}}}}}
Ejercicio 6:
Simplificar
\huge{H=\sqrt[{\sqrt[\sqrt{2}]{4}}]{2^{2^{\sqrt{2}}}}}
Ejercicio 6:
Simplificar
\huge{H=\sqrt[{\sqrt[\sqrt{2}]{4}}]{2^{2^{\sqrt{2}}}}}

7 – Al resolver
\Large{n^{n}=\left ( n^{2} \right )^{n^{2}}}
La suma de los valores de 'n' es:
Ejercicio 7:
Al resolver
\LARGE{n^{n}=\left ( n^{2} \right )^{n^{2}}}
La suma de los valores de 'n' es:
Ejercicio 7:
Al resolver
\LARGE{n^{n}=\left ( n^{2} \right )^{n^{2}}}
La suma de los valores de 'n' es:

8 – Hallar el valor de 'a':
\small{a^{2+a^{2+a^{2+a^{2+\cdots }}}}=\sqrt[3]{a^{8}\sqrt[3]{a^{8}\sqrt[3]{a^{8}…}}}}
Ejercicio 8:
Hallar el valor de 'a':
\LARGE{a^{2+a^{2+a^{2+a^{2+\cdots }}}}=\sqrt[3]{a^{8}\sqrt[3]{a^{8}\sqrt[3]{a^{8}…}}}}
Ejercicio 8:
Hallar el valor de 'a':
\LARGE{a^{2+a^{2+a^{2+a^{2+\cdots }}}}=\sqrt[3]{a^{8}\sqrt[3]{a^{8}\sqrt[3]{a^{8}…}}}}

9 – Resolver
\Large{\left ( \sqrt[x^{-1}]{\frac{1}{x}} \right )^{\sqrt{x^{-1}}}=\sqrt[\sqrt{5}]{5}}
e indicar el valor de:x^{-1}
Ejercicio 9:
Resolver
\LARGE{\left ( \sqrt[x^{-1}]{\frac{1}{x}} \right )^{\sqrt{x^{-1}}}=\sqrt[\sqrt{5}]{5}}
e indicar el valor de:x^{-1}
Ejercicio 9:
Resolver
\LARGE{\left ( \sqrt[x^{-1}]{\frac{1}{x}} \right )^{\sqrt{x^{-1}}}=\sqrt[\sqrt{5}]{5}}
e indicar el valor de:x^{-1}