Temas disponibles:
Vectores I
A continuación se muestran algunos ejercicios de vectores en diferentes niveles de dificultad.
Ejercicios de vectores
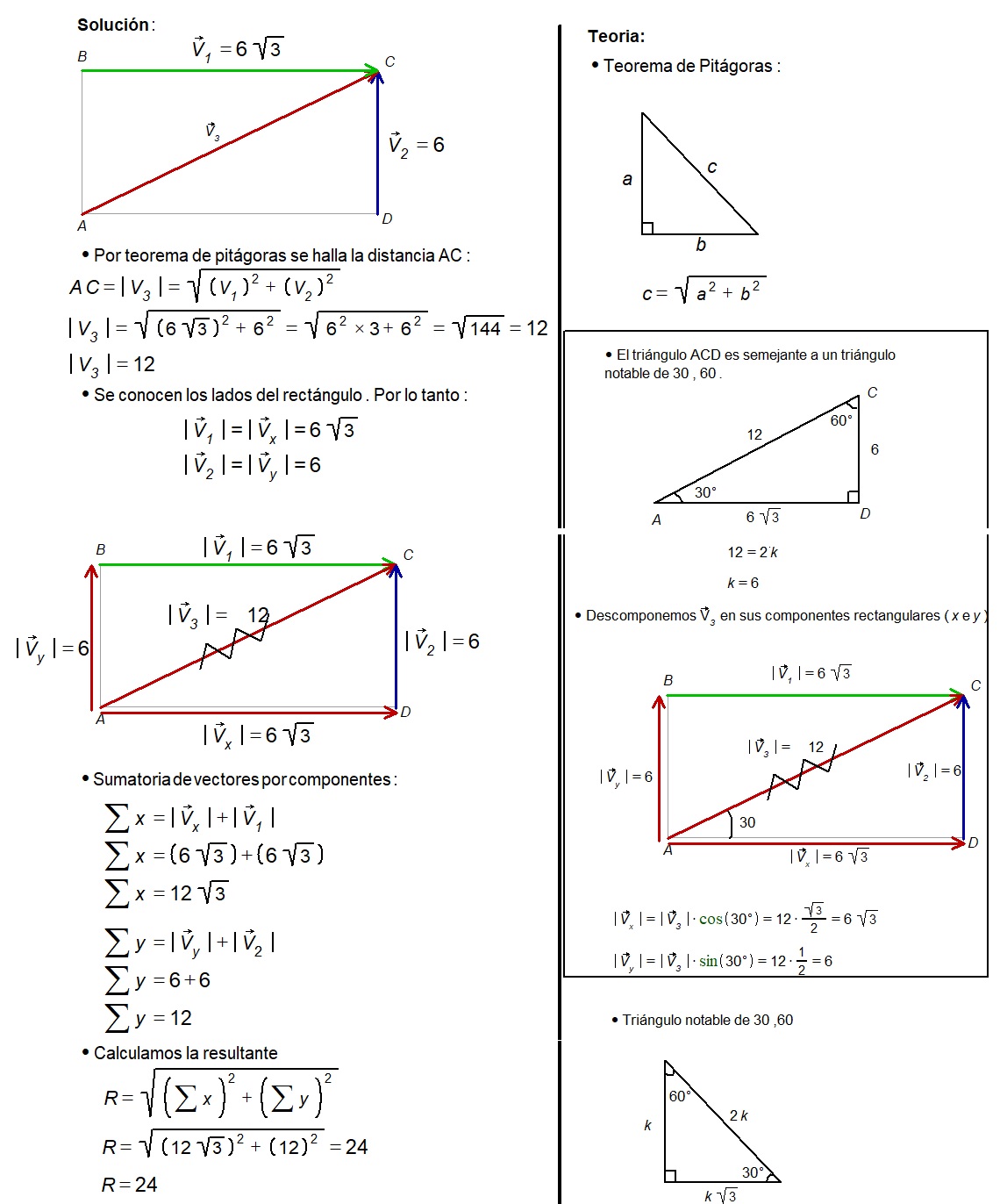
1 – Hallar el módulo de la resultante de los vectores indicados, si ABCD es un rectángulo, tal que BC=6\sqrt{3} y CD=6.
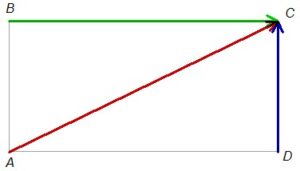
Ejercicio 1:
Hallar el módulo de la resultante de los vectores indicados, si ABCD es un rectángulo, tal que BC=6\sqrt{3} y CD=6.
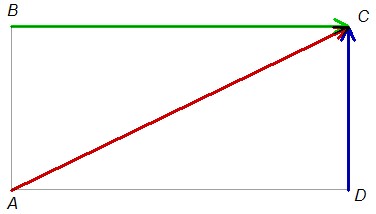
Ejercicio 1:
Hallar el módulo de la resultante de los vectores indicados, si ABCD es un rectángulo, tal que BC=6\sqrt{3} y CD=6.

2 – Siendo la figura un hexágono regular de lado 7 unidades, determinar el módulo de la resultante de los vectores mostrados.
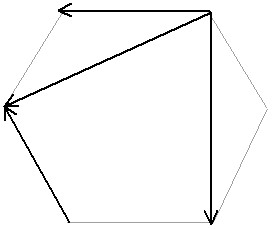
Ejercicio 2:
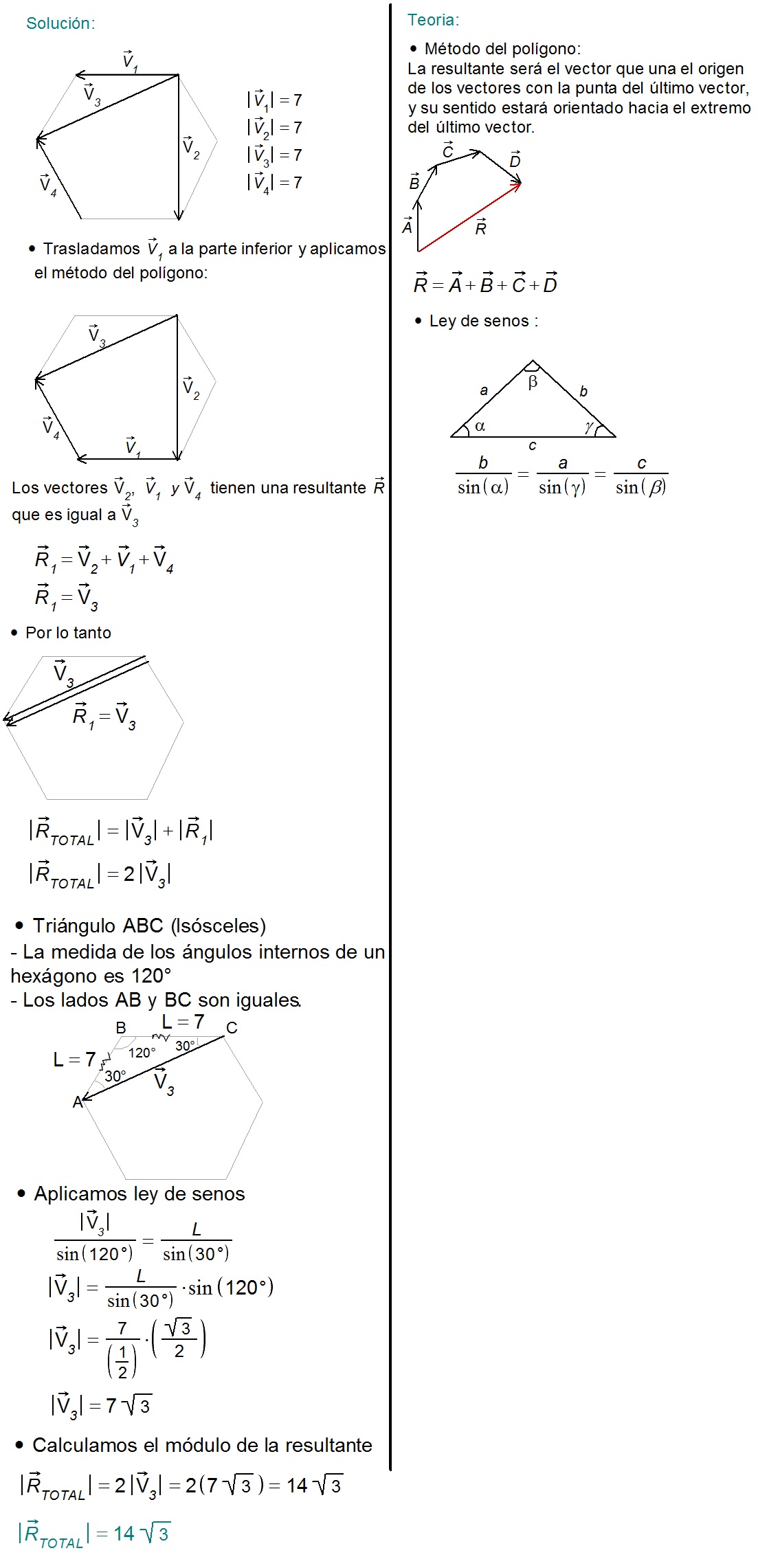
Siendo la figura un hexágono regular de lado 7 unidades, determinar el módulo de la resultante de los vectores mostrados.

Ejercicio 2:
Siendo la figura un hexágono regular de lado 7 unidades, determinar el módulo de la resultante de los vectores mostrados.

3 – Los puntos A, B y C determinan un triángulo equilátero de 2m. Hallar el módulo del vector resultante.
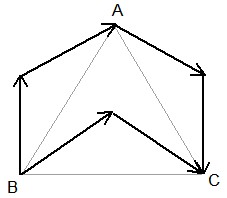
Ejercicio 3:
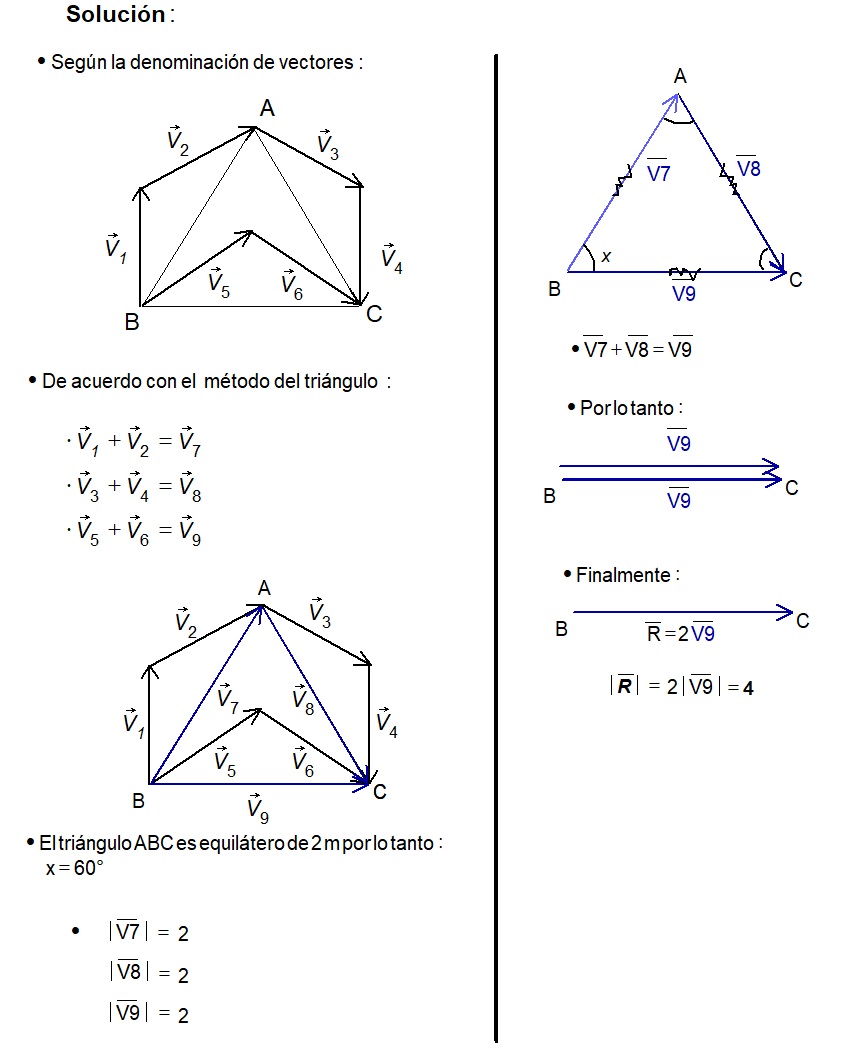
Los puntos A, B y C determinan un triángulo equilátero de 2m. Hallar el módulo del vector resultante.

Ejercicio 1:
Los puntos A, B y C determinan un triángulo equilátero de 2m. Hallar el módulo del vector resultante.

4 – Si: | \vec{P} |=\sqrt{2} y | \vec{Q} |=1
y el ángulo formado por
dichos vectores es 60º. Hallar el coseno cuadrado del ángulo formado por los vectores
\vec{P}+\vec{Q}=1 y \vec{P}-\vec{Q}.
Ejercicio 4:
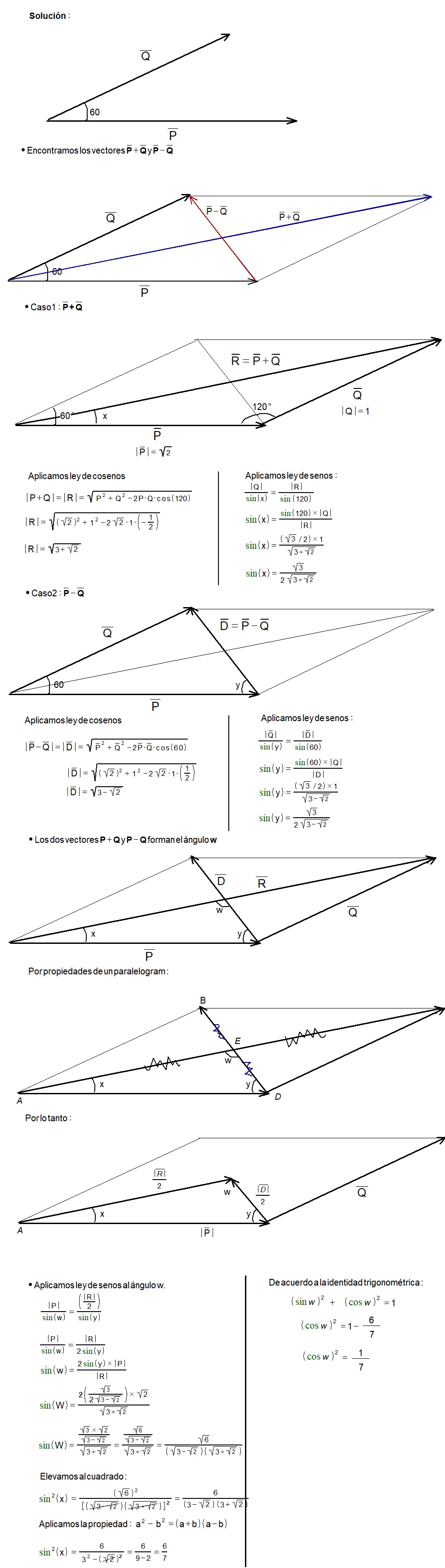
Si: | \vec{P} |=\sqrt{2} y | \vec{Q} |=1
y el ángulo formado por dichos vectores es 60º. Hallar el coseno cuadrado del ángulo formado por los vectores \vec{P}+\vec{Q}=1 y \vec{P}-\vec{Q}.
Ejercicio 4:
Si: | \vec{P} |=\sqrt{2} y | \vec{Q} |=1
y el ángulo formado por dichos vectores es 60º. Hallar el coseno cuadrado del ángulo formado por los vectores \vec{P}+\vec{Q}=1 y \vec{P}-\vec{Q}.
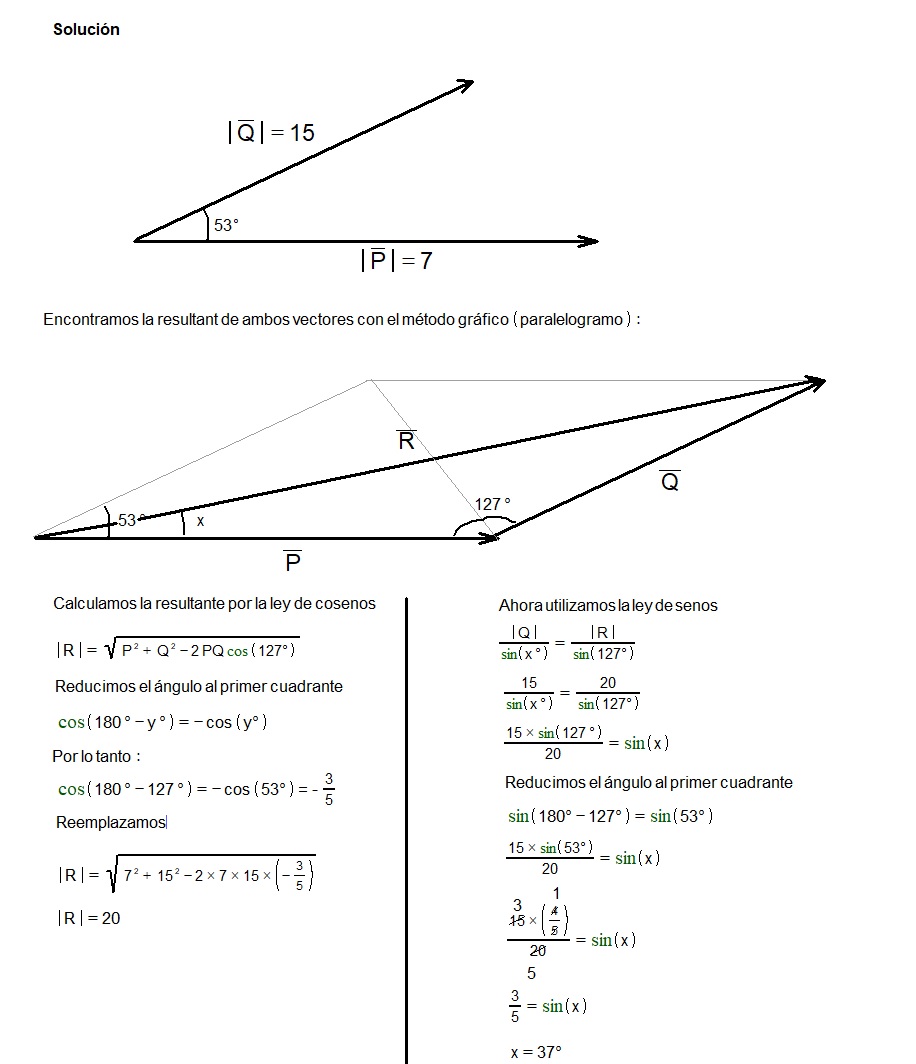
5 – Se tienen dos vectores de 7 y 15 unidades que forman entre si un ángulo de 53°, hallar el ángulo entre la resultante y el menor vector dado.
Ejercicio 5:
Se tienen dos vectores de 7 y 15 unidades que forman entre si un ángulo de 53°, hallar el ángulo entre la resultante y el menor vector dado.
Ejercicio 5:
Se tienen dos vectores de 7 y 15 unidades que forman entre si un ángulo de 53°, hallar el ángulo entre la resultante y el menor vector dado.
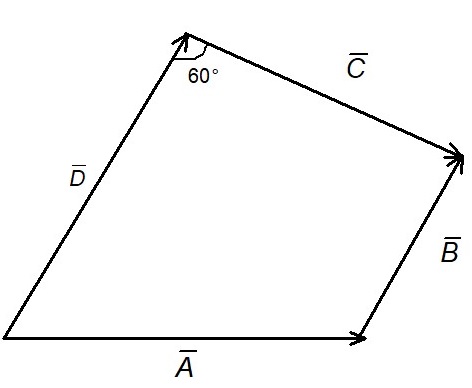
6 – Se muestran los vectores \vec{A},\vec{B},\vec{C},\vec{D} , hallar ‘x’ si:
x=|\vec{A}+\vec{B}+\vec{C}+\vec{D}|, además D=8 y C=3.
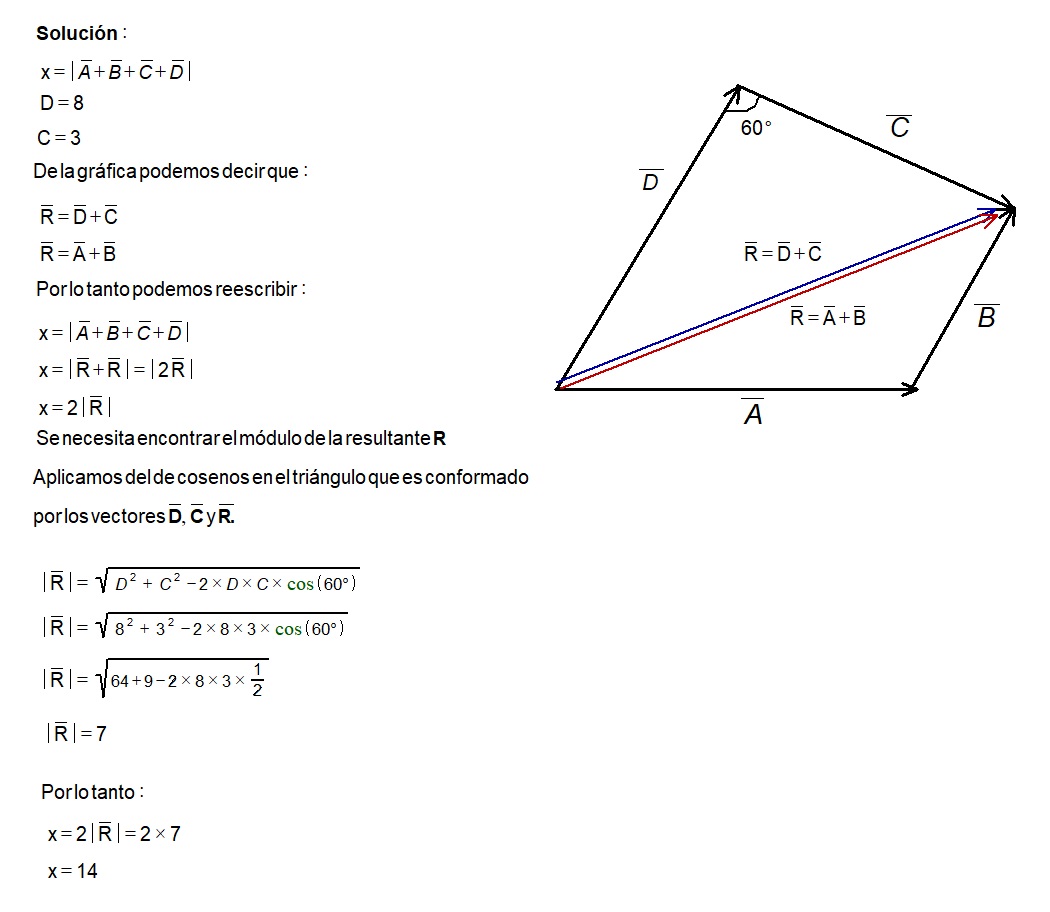
Ejercicio 6:
Se muestran los vectores \vec{A},\vec{B},\vec{C},\vec{D} , hallar ‘x’ si:
x=|\vec{A}+\vec{B}+\vec{C}+\vec{D}|, además D=8 y C=3.

Ejercicio 1:
Se muestran los vectores \vec{A},\vec{B},\vec{C},\vec{D} , hallar ‘x’ si:
x=|\vec{A}+\vec{B}+\vec{C}+\vec{D}|, además D=8 y C=3.
7 – En la figura, determinar el módulo del vector resultante del conjunto de vectores mostrado, si el radio de la circunferencia es de \sqrt{5} unidades y O es su centro.
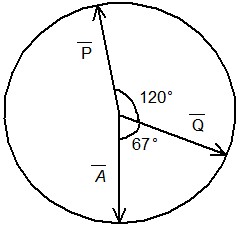
Ejercicio 7:
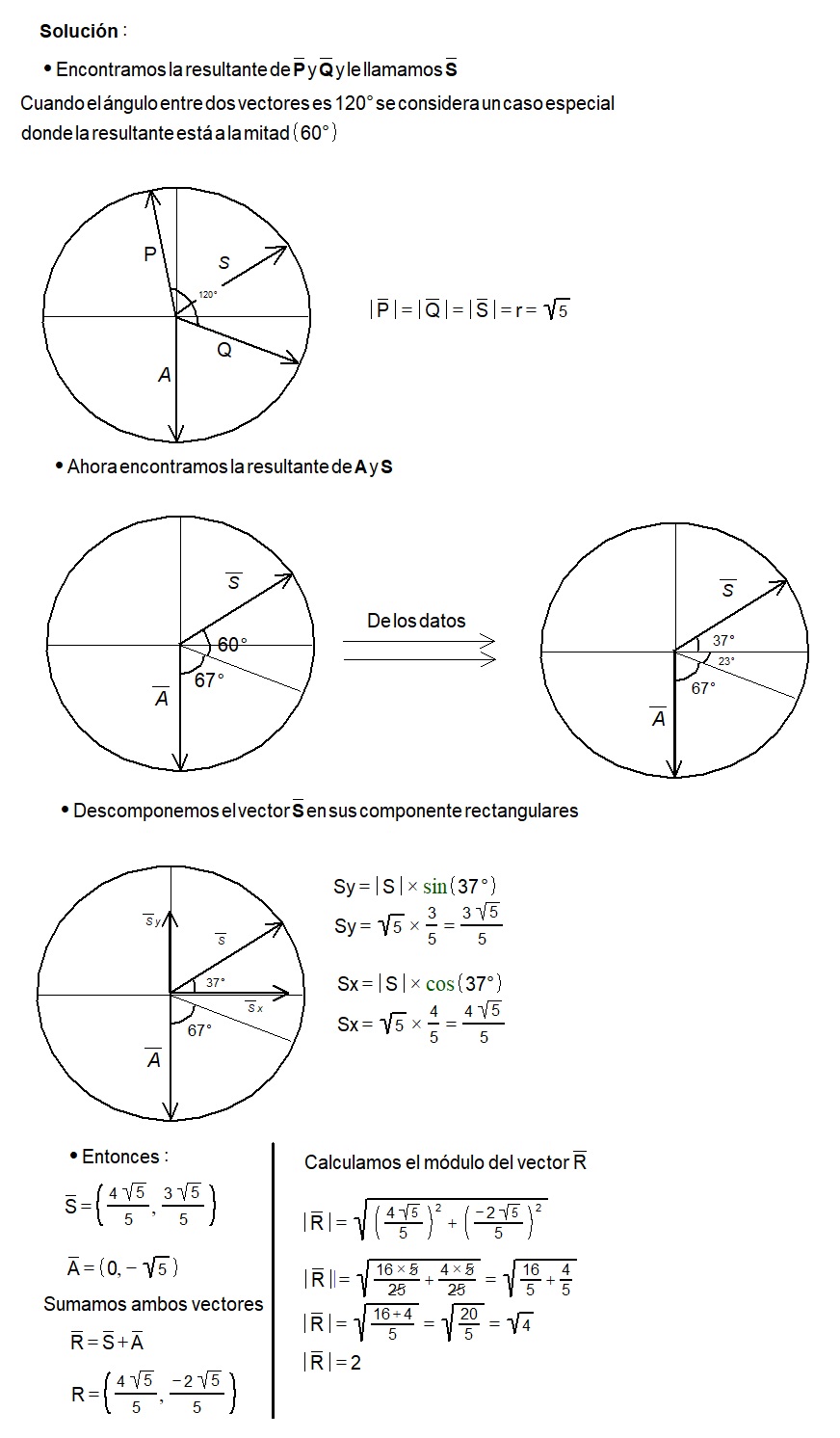
En la figura, determinar el módulo del vector resultante del conjunto de vectores mostrado, si el radio de la circunferencia es de \sqrt{5} unidades y O es su centro.

Ejercicio 1:
En la figura, determinar el módulo del vector resultante del conjunto de vectores mostrado, si el radio de la circunferencia es de \sqrt{5} unidades y O es su centro.
8 – En el cuadrado M y N son puntos medios. Hallar \vec{x} en función de \vec{a} y \vec{b}.
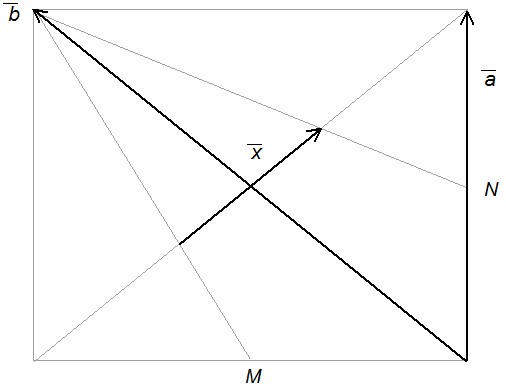
Ejercicio 8:
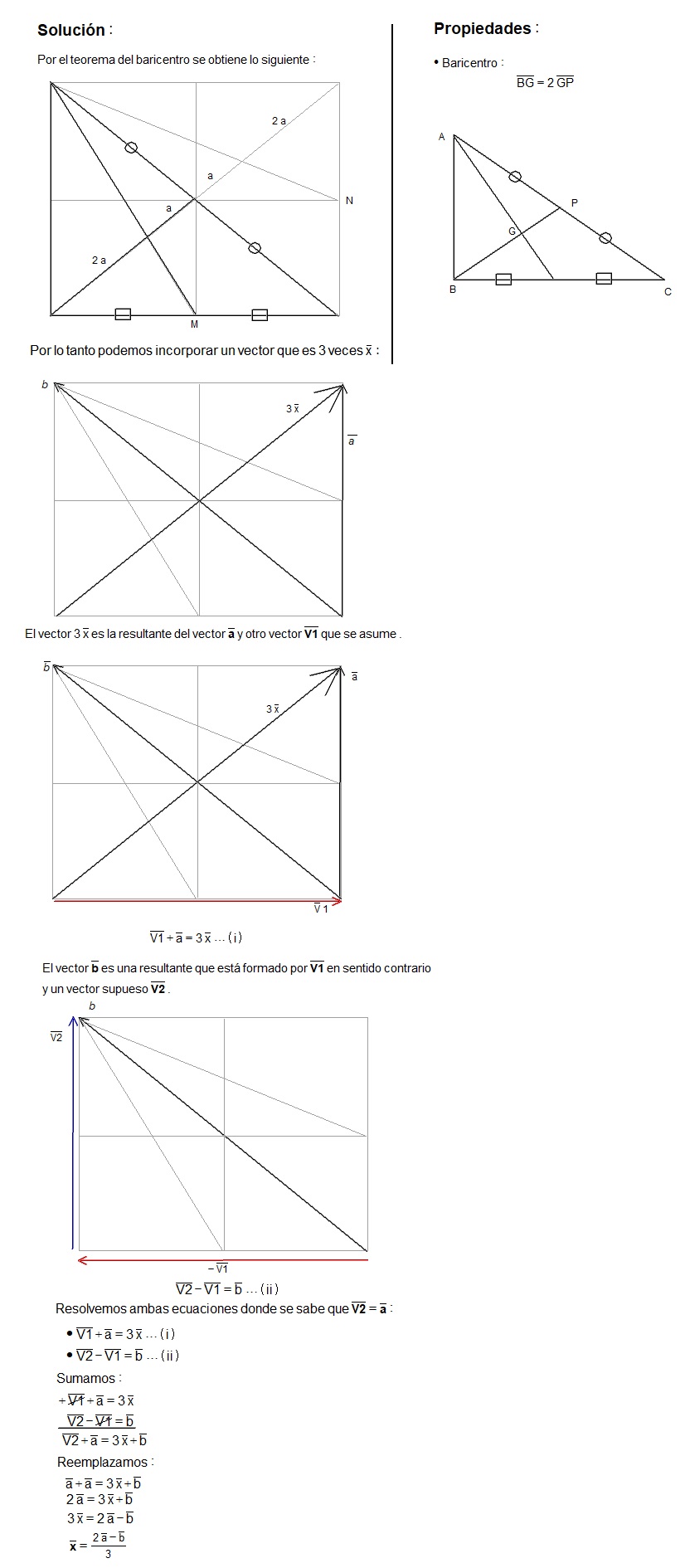
En el cuadrado M y N son puntos medios. Hallar \vec{x} en función de \vec{a} y \vec{b}.

Ejercicio 2:
En el cuadrado M y N son puntos medios. Hallar \vec{x} en función de \vec{a} y \vec{b}.

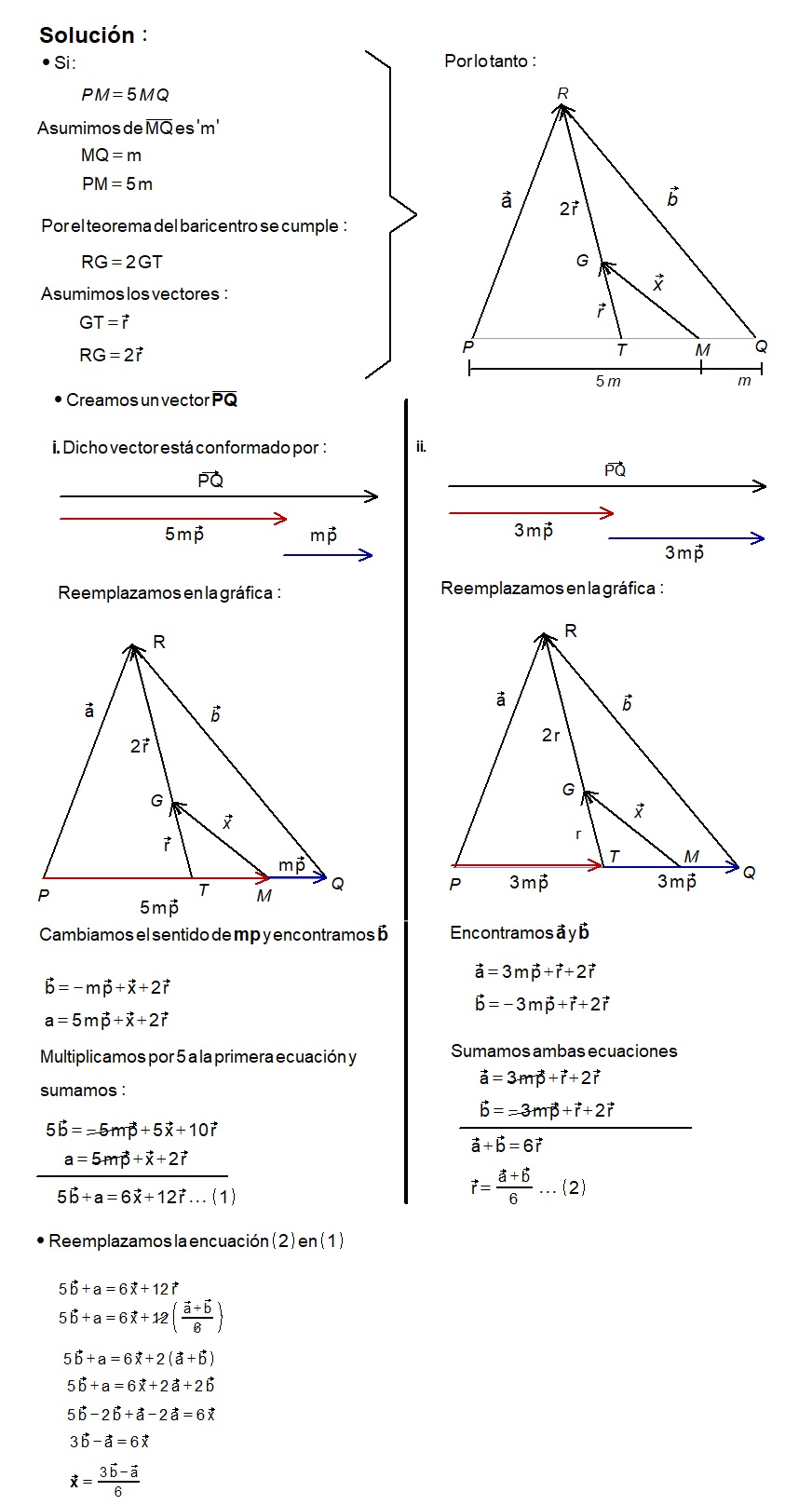
9 – Determine \vec{x} en función de \vec{a} y \vec{b} , sabiendo que PM = 5MQ y G es el baricentro del triángulo PQR.
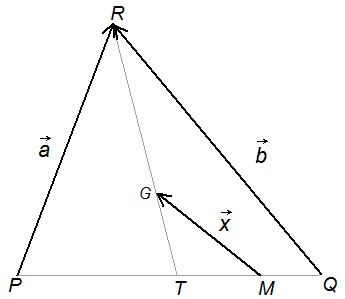
Ejercicio 9:
Determine \vec{x} en función de \vec{a} y \vec{b} , sabiendo que PM = 5MQ y G es el baricentro del triángulo PQR.

Ejercicio 1:
Determine \vec{x} en función de \vec{a} y \vec{b} , sabiendo que PM = 5MQ y G es el baricentro del triángulo PQR.